Sidney J. Chapman's 1909 address on the "Hours of Labour" was considered the "classical statement of the theory of 'hours' in a free market", (J.R. Hicks, Theory of Wages, 1932). Then it virtually vanished from the economics discourse. Why?

From S.J. Chapman's Hours of Labour (Economic Journal, September, 1909, footnote 1, pp. 363-365) new graphs added by Tom Walker, May 1999.

The argument in the more technical parts of this address, concerned with the determination of the length of the working day, may be conveniently summarized with the aid of the following figure[s]. In order to avoid the complexities arising from the redistribution of labour between the industries of a country, suppose that only one industry exists. Measure units of time in the working day along OX, and units of money along OY.

Consider first the unbroken lines which represent the influences governing employers. The curve P expresses the long-period variations with the length of the working day of the marginal value of a fixed quantity of labour: the opinion that these can be represented by a curve has been defended in the body of this address. If On hours are worked, this daily value of labour and the wage will ultimately be Onda; if Ob hours are worked, this value and wage rises to Oba; if Oe hours are worked, it falls to Oba - bef.

The meaning of the curve P will now be plain. The curve is supposed to rise in the first instance because increasing the daily hours of labour would at first raise the level of efficiency, and if it did not, the larger wage would. But P must begin to fall at some point, and eventually cross OX, as is demonstrated in the body of the address. Actually, of course, P could not start at OY, because a man when engaged for only a fraction of his time daily could not live on the proceeds of his work, but it has been so drawn in the figures to enable us to picture the value and wage of labour by the area between the curve P and the co-ordinates.

The curve ck represents the immediate variations of the marginal value of a fixed quantity of labour with the length of the working day on the assumption that the normal working day has been Ob. Hence the value of the normal product of the last minute of the working day Ob is bg. Ex hypothesi Obgc must equal Oba. If the working day is lengthened to Oe the product will at first be augmented by bekg, but finally by a gradual decline it will sink to Oba-bef.

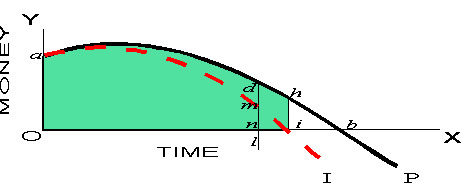
The influences guiding the operatives are expressed in the dotted lines, the meaning of which must now be explained. Draw any vertical line dl to the left of b. Then dn is the addition made in the long run to the money income of the operative when the Onth increment of time is added to the working day. Let dm be the long-period value to the operative, when his income is Onda, of the leisure destroyed by the addition of the Onth increment of time to the working day. The curve I is the locus of the point m. Evidently, starting at a, it will lie throughout its length below P, increasingly departing from P (because leisure is subject to the law of diminishing utility and the value of leisure rises with income), and cut OX to the left of b.

Apart from the satisfaction or dissatisfaction of working, therefore, the far-sighted operative who took into account the value of leisure would choose a normal day Oi, which is less than Ob (the choice of far-sighted employers in combination). When the normal day is Oi the marginal value of leisure to an operative with a wage Oiha would be ih, which equals the long-period marginal earnings attributable to the Oith increment of time in the working day.

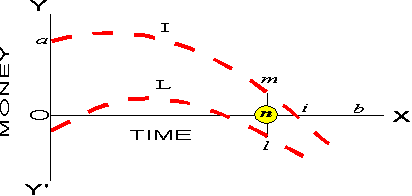
Now, let L indicate the long-period values to the operative of the effects of different lengths of working day on the absolute satisfaction or dissatisfaction involved in the labour itself, L being otherwise interpreted, when units of money are measured along OY' as well as along OY, and the parts of the curve below OX indicate the prices which would be paid to escape the dissatisfaction involved in working, and the parts above OX the money value of the satisfaction involved in working. As some of the time devoted to production will probably be pleasant to the operative when the length of the working day is most favourable to his enjoyment of work, we may assume that L need not lie throughout its length below OX. Then the working day which perfectly wise operatives would choose would be On, the point n being such that nm = nl, the attainment of which equation is the condition under which the operative's satisfaction is maximised. If, as is theoretically conceivable but practically impossible, L lay further above OX for the abscissa Ob than I lay below it, the length of day most advantageous to the operative would be greater than Ob.

If normal hours are On, the operative who lives for the day and is aware that more work, measured by results, means proportionately more pay, will obviously desire hours longer than On for the following reasons. The product attributable to the Onth increment of working time is greater than dn, since dn represents the gain resulting from the Onth. less the loss occasioned by the reduction which will ultimately take place in the productivity of the operative's earlier hours in consequence of the addition of the Onth increment of time to the working day. For similar reasons the short-period or immediate value of leisure might be less than dm. Again, the money measure of the disutility of the Onth increment of working time is less than nl, because nl measures the results from the fact that the Onth increment of working time diminishes capacity in earlier hours to enjoy labour or sustain fatigue.

It is evident, therefore, that a balance of gain accrues to the operative from the work of the Onth unit of time, when everything, including wages is taken into account, but the effect of the work on the Onth unit of time on the gain associated with the rest of the working day ignored; and, further, that the balance of gain attributable to the Onth hours will not disappear, though it may contract if the working day be slightly extended. Hence we must conclude that operatives who are not alive to the reactions of long hours on efficiency and capacity to enjoy life and work will tend to choose a longer working day than is wise from their point of view. However, to repeat, they will not approve such long hours as employers who are equally blind to future reactions, because the latter, if purely self-interested, make no allowance for the disutility of labour to the operative or the utility to him of leisure.

In the event of progress in methods of production the new position of P would be such that the area enclosed between it and the co-ordinate axes would be increased. P in its new position might cut OX at b, but in all probability the new intersection with OX would be to the left of b. It is not likely to fall to the right of b, since improvements in the mechanical aids of labour seldom mean that work is rendered less exhausting.

Even if the new curve P passed through b, the new position of I would practically mean its intersection with OX to the left of i because of the enhanced value of leisure. Further L, though it might rise higher than before, would probably descend sooner and at least as steeply. It is to be observed in addition that but for interest, rent and heavy depreciation charges, industrial progress would bring about movements of P involving more considerable augmentation of the area contained between P and the co-ordinate axes.

Improved education, apart from its effect on efficiency, would bring about a subsidence of the curve I, so that in its new position it would cut OX to the left of i. The effect wrought by progress on short-period forces need not be worked out in detail. The general conclusion is manifest that progress may be expected to be accompanied by a progressive curtailment of the working day.